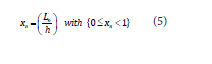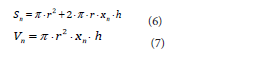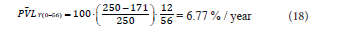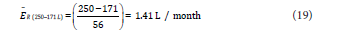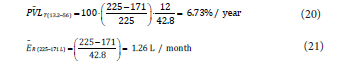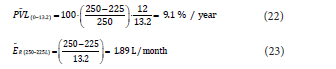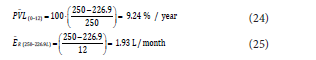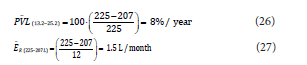¹ Santiago de Cuba rum factory, Santiago de Cuba, Cuba
² Analytical and Circular Chemistry, Hasselt University, Agoralaan, building D, 3590 Diepenbeek. Belgium
³ Centre of Neurosciences Signal and Images Processing, Applied Acoustic Research Group, Universidad de Oriente, Santiago de Cuba, Cuba

*Address for Correspondence: Jan Yperman, Analytical and Circular Chemistry, Hasselt University, Agoralaan, building D, 3590 Diepenbeek. Belgium E-mail Id: jan.yperman@uhasselt.be

Submission: 16 August 2023 Accepted: 11 September 2023 Published: 15 September 2023

Copyright: © 2023 Del Toro Del Toro N, et al. This is an open-access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium provided the original work is properly cited.

Keywords: Rum; Barrel; Maturation; Surface Area to Volume Ratio; Optimization; Volume Loss

In this work, the behavior of the surface area to volume ratio (s/v) in five types of standard casks for rum ageing is mathematically modeled in function of the liquid volume. The (s/v) variation is discussed and compared between the two barrel storing systems in cellars (vertical and horizontal). The ratio is applied as a parameter to obtain an optimized criterion for filling volume and re-filling time of wood casks during the long-term rum maturation process focused on volume loss reduction and barrels preservation. An example of re-filling time calculation and volume loss assessment for rum ageing in a traditional 250 L hogshead barrel is presented and debated.

Rum is a distilled beverage obtained from the fermentation of sugar cane molasses, a sub-product from the sugar cane production. For the specific case of the rum produced in Cuba, the fresh distilled spirit (known as “Aguardiente”) is a translucent, shiny, full-bodied drink with no suspended particles. The production process comprises the following fundamental stages: (I) Growing of sugar cane, (II) Obtaining the molasses from sugar cane production process (III) Molasses fermentation (usually within 24-26 h of fermentation time), (IV) Distillation (column system in a continuous processis applied), (V) Natural Ageing/Maturation in white oak (Quercus Alba) wood during a timed period in order to improve its organoleptic characteristics and (VI) Mixing [1,2]. In the case of high-quality products, at least two ageing stages are required. The first corresponds to the original spirit (Aguardiente). The second corresponds to the ‘base rum’, which consists of a mixture of aged spirits with a distillate for rum (both filtered through activated carbon) and purified water. In the specific case of extra aged rums, the use of a certain proportion of ‘base rum’ that has undergone a third ageing stage is required.

The inclusion of additional ageing stages is optional and is left to the discretion of the Cuban rum masters. During the ageing stages, the Cuban rum masters pay special attention to the sensory attributes of the aged spirit, as it is a decisive element in determining the sensory profile of the future rum. Among other aspects, they have to select the characteristics of the barrel (white oak, size and period of time in use) employed for each of the stages in the ageing process (two as a minimum) in order to achieve the typical sensory profile required for each of the stages [1]. Throughout the ageing process, a series of reactions take place resulting in changes in chemical composition and organoleptic properties of the rum. These changes will give rise to modifications in its final quality, due to the complex aroma from wood. Two variables are fundamental in the ageing process: the ageing time and the quality of the barrel wood. Barrels are directly involved in the produced changes on rum’s composition due to the transfer of oxygen and phenolic and aromatic compounds from wood to rum [1-11]. Barrels have another important function than those of serving as a container. An oak barrel acts as an active vessel that reacts and releases chemical compounds into the rum, improving its physical, chemical and sensory properties. Depending on its origin, age, thickness, uses, roasting, size and the contact time, the acquired properties are different [1,3,12-14]. Wood barrel ageing improves not only color and mouthfeel, but also increases aroma complexity due to the extraction of compounds present in the wood. These compounds include cellulose, hemicellulose, lignin, acids, sugars, terpenes, volatile phenols and lactones [3,12-14]. Therefore, an ageing period in the wooden barrel is required to attain sensory fullness and high quality. Despite its many advantages, natural ageing in barrels has several drawbacks. Barrels are expensive to produce, have limited lifetime and generate a significant volume loss due to liquid evaporation [2]. The blends of spirits and the different base rums used in each of the stages of the ageing process, carried out under the guidance of the Cuban rum master, are decisive in achieving the finished rum with proper sensory characteristic balance of taste, color and aromas.

In Cuban rum cooperage technology, used whisky barrels are generally applied for rum maturation since the barrel wood exchange/extractable compounds have been already lowered by a previous contact with whisky. Thus, rum technology is more focused on potentiating the oxidation ageing mechanisms in long-term aged products [12-14]. In cooperage technology, the volume loss during ageing depends basically of the wood permeability, which is defined as the ability of the wood to allow fluid flow to pass through it without altering its internal structure. In general, fluid flow through wood can occur in two ways: (1)As in a porous solid following Darcy’s law (the bulk flow of fluids through the interconnected voids of the wood structure under the influence of a static or capillary pressure gradient) and (2)Due to diffusional mechanisms, also known as permeation. In turn, diffusion may occur as inter-gas diffusion, which includes the transfer of water vapor through the air in the wood cell lumen, and bound water diffusion, which occurs inside the cell walls of the wood [4]. In the complex case of an oak wood barrel stave during rum ageing, both phenomena occur simultaneously. The liquid (as bulk flow) penetrates into the wood, which is a porous solid, due to the hydrostatic pressure of the liquid, causing the water vapor and ethanol from the rum inside and the oxygen from the air outside to diffuse through the wood due to the concentration difference between the inside and outside of the barrel [15-18]. In this manner, the evaporation of the liquid (volume loss) through the wood barrel occurs in two phases: an initial phase or transition state in which wood is impregnated until a steady state is achieved and a second phase or steady state in which the impregnation flow entry of fluid into the wood has the same magnitude as the evaporation outflow to the exterior [4].

The volume loss is an intrinsic part of the ageing process. As previously described, the barrel acts as a semi-permeable membrane that allows evaporation from the cask and migration of air into the barrel, because of its porous structure [2].

The volume loss during maturation strongly depends on external factors related with the climatic conditions of the cellar such as air humidity, velocity and temperature. But also, internal factors corresponding to the wood and liquid properties (wood porosity/ permeability, density, stave preparation and morphology of the wood fiber), as well as the alcohol content of the liquid, its density and viscosity have a significant influence [2,19-21]. The evaporation loss during the ageing process is an indubitable economic concern for spirit producers. Therefore, efforts to diminish and/or control the loss during ageing are crucial in order to optimize the production process and to reduce the associated costs [2].

Apart from the external and internal factors previously mentioned that influence evaporation during spirit ageing, one of the most important aspects is the barrel size. The percent volume evaporated from the barrel increases as a direct function of the cask surface area to volume ratio (s/v) expressed in m² of wood surface per m³ of liquid volume in the barrel [19,21].

Production economy favors the larger size barrels due to the large storage capacity per surface of the wood and less evaporation rate during ageing, whereas ease of movement and earlier maturation are favorited by a smaller size [22-25]. A compromise between these opposite aspects has led to the adoption of barrels with a capacity ranging between 200 and 500 L in spirits such as whisky and rum. The ratio of (s/v)most used traditional barrels of 200-250 L is roughly calculated at (s/v)= 9 m-¹ which is equivalent to 90 cm² /L [26]. Due to its significant (s/v) importance for alcoholic beverages technology, the effect of ratio during the ageing process has been widely debated in several publications [22-26]. In that sense, experiments have been conducted in order to study the influence of different barrel sizes during the ageing process of spirits and wine, focused mainly on the chemical/sensory profile and evaporation loss [2,22-26].

However, in the case of spirits with long ageing periods (more than 3 years of maturation) as the volume of the liquid in the barrel decreases due to the evaporation, the wetted surface area by the liquid into the barrel also changes. Therefore, opposite to the traditional consideration that the (s/v) ratio in the barrel is a constant value, this ratio actually changes in function of the ageing time.

Following this approach, the (s/v) ratio of any barrel will be ranging from a constant value (barrel completely filled) which certainly depends on the cask size and a final value that will tend to infinity when the volume of the liquid contained in the barrel tends to zero. This will be mathematically demonstrated further on.

Based on that, it can be the case that two barrels of different sizes might have equal (s/v) ratio at certain volume (filling level) of liquid. In addition, as extensively reported [2,14-26], the change of (s/v) ratio in a wood barrel influences not only the wood-liquid chemical interaction and ageing reaction kinetics but also the volume loss. The higher the (s/v) ratio (like in small barrels), the higher is the percent of volume loss and the faster the ageing process [2, 12-18, 22-26]

So far, no references were found concerning to the discussion of the change of (s/v) ratio in function of the liquid level in a barrel during the ageing process. Specifically, for the long-term spirits maturation (and especially in tropical countries) the barrels suffer a significant reduction of its liquid volume due to evaporation with an average volume loss ranging from 6-13% per year depending on the climatic conditions in non-conditioned cellars [2].

In cellars, barrels can be stored for spirits maturation in vertical or horizontal position as presented in [Figure 1a,b] respectively. In order to increase the storing/logistic efficiency of the cellar’s space, spirit producers have introduced the palletized system of ageing which consist on storing the barrels in vertical position and supported by pallets.

Palletized strategy has advantages compared with the traditional racked ageing system (barrels horizontally stored). The vertical arrangement not only increases the volume storage yield (L/m²) up to 20% but also improves the work dynamics in the cellar, which in turn impact significantly on the logistic/production capacity of the spirit manufacturing. However, after many years of using the traditional rack system of ageing, volume loss is still under assessment for rum ageing in palletized system. The barrel geometry influences the production processes, the cost of the barrel and its storage and consequently, the added value of the rum [27].

Several mathematical methodologies have been applied to geometrically describe the wood barrels used in wine and spirit industry. Until today, tradition has passed the use of empirical and simplified formulas that relate the barrel volume to the following shape parameters: belly diameter, head hoop and length or even the distance from the bunghole to the head/bottom corner. Ten empirical and simplified formulas have been reported for barrel volume calculation [27].

Although the error of employing these formulas fluctuates in the range of 4-10% between them [27], its main advantage is their simplicity which is a very suitable aspect for practical purposes in cooperage and cellar management. Additionally, very dedicated and more complex methods to describe barrel geometric parameters such as 3D modelling, finite differences method and evolution of a circumference arc through the infinitesimal calculus have been reported [27]. Both, empirical and complex models are used for the economic optimization of the barrel, connected with the (s/v) ratio. On the other hand, as the barrel continuously loses liquid due to evaporation, along the time, the upper staves eventually are not wetted by the liquid. So, in time, if the volume liquid is low enough, the head space barrel wood dries out, the stave joint separation increases and the cask becomes less hermetic. At this point, the barrel suffers a progressive deterioration of its mechanical integrity, ageing efficiency and in the worst scenario, an irreversible damage.

Therefore, this problem can be avoided if the barrel is re-filled with liquid of the same maturation time to reach again an adequate liquid volume. The cask re-filling process is a common managing strategy in cellars during long-term rum ageing not only to protect the cask from deterioration but also to optimize the cellar storage efficiency.

In Cuban rum technology, at a certain volume of liquid, the content of partially filled casks with the same aged product is used to complete the cask volume at the original level, thus emptied ones can be efficiently recovered back to the process cycle. Based on that, for spirits manufacturers which manage very aged products under natural ageing technology, it is a continuous concern to find the optimal re-filling time of the casks.

In general, the re-filling time is in general empirically determined according to the experience of the specialists and based on the specific conditions of the cellar. In this work, the behavior of the (s/v) ratio in function of the liquid volume in five types of standard casks for rum ageing is mathematically modeled. The change of (s/v) ratio with the liquid volume is discussed and compared between the two barrel storing systems in cellars (vertical and horizontal). The (s/v) ratio is applied as parameter to obtain an optimized criterion for filling volume and re-filling time of wood casks during the long-term rum maturation process focused on volume loss reduction and wood barrels preservation. The presented study might be useful not only for rum producers but for other specialists and researchers in the production of aged spirits.

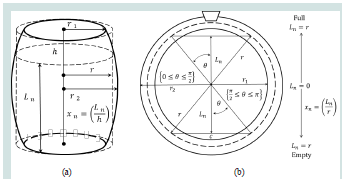
The cask geometric shape is a truncated prolate spheroid with circles of equal radius in top and bottom (head size). The end radius, commonly defined as the “Head / Top radius” is presented in Figures 1 (a) and (b) as r₁. On the other hand, the “belly radius / bilge size” r₂ is the radius of the widest circumference formed by the spheroid [28]. The total volume and surface area of a cask can be determined by Eqs. (1) and (2) respectively assuming it has an equivalent cylinder of radius (r) of the truncated prolate spheroid (this simplified mathematical approach has been reported as one of the more accurate models with about 5% of error) [27]. thus

The (s/v)₀ ratio corresponds to a fix value which is indeed characteristic for each barrel depending on its size and geometric proportions.

When the barrel is full of liquid, the internal wall of the cask is completely wetted. When the liquid evaporates during ageing, in a discrete level point “n”, the liquid volume as well as the wetted surface in the cask will vary in different orders, so the initial (s/v)₀ will change to another (s/v)_n value in function of the liquid level/volume.

Analyzing the simpler case of vertical barrel position[Figure 1a] and considering the barrel’s geometry as an equivalent cylinder of radius (r), the liquid volume variation is a linear function of the liquid level (L_n). Then, any liquid level (liquid volume) in the barrel at a discrete point “n” can be expressed as a fraction (x_n) of the total barrel height as

However, when the barrel loses liquid (it is not full anymore) the upper head is not wetted in vertical position, therefore ( n 0 S ≠ S ) and equations (1) and (2) can be transformed as an xn function in order to calculate the wetted surface and the volume of liquid in a discrete level point “n” as

S_n: Wetted internal surface area of the barrel at a level point “n” (in m^₂)

V_n: Liquid volume contained in the barrel at a level point “n” (in m³)
x_n: Fraction of liquid level at a discrete point “n”(dimensionless)
L_n: Liquid level in the barrel at a discrete point “n”(in m)
Consequently, by combining Eqs. (5), (6) and (7) gives for vertical position

(s/v)_n: Surface area to volume ratio at a specific liquid level/volume discrete point “n” (in m-1) From Eq. (8) it can be defined that lim n xn (SV)_n → = ∞ therefore it is confirmed that the (s/v)ⁿ ratio increases as an inverse function of the liquid level into the cask.

The mathematical modeling of the (s/v)_n in function of the fraction of liquid level in the horizontal position of the cask (Figure1 (b)) is somewhat more complex to obtain. In the circumferential geometry, the fraction of liquid level is not a linear function of the liquid volume as presented in the vertical position. In this case

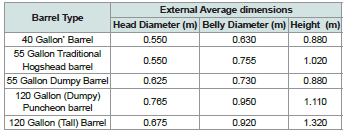
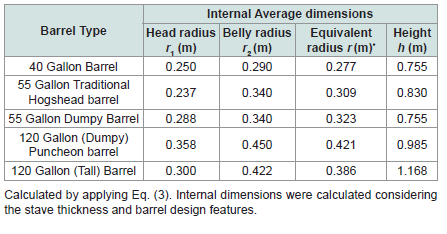
Five types of whisky barrels with capacities ranging from 40- 120 UK Gallons (182-545 L), typically used in rum industry, were evaluated. [Table 1] presents the external average dimensions of the assessed casks. On the other hand, [Table 2] depicts the internal average dimension calculated by considering the staves thickness (ranging from 25-32 mm) and barrel design features.

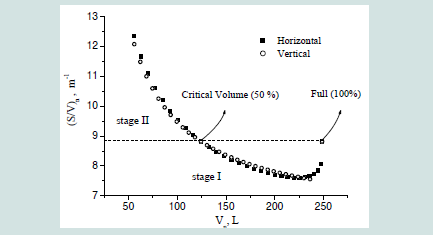
[Figure 2] presents a comparative plotting of the (s/v)_n ratio in function of the liquid volume at the two different storage positions of the barrel: horizontal and vertical from 250 (full) to 25 L. Practically the same behavior of (s/v)_n ratio was observed with minor differences between vertical (using Eqs. (4-8)) and horizontal positions (using Eqs. (9-15)) of the assessed traditional hogshead whisky barrel. All the studied barrels [Table 1 and Table 2] presented the same pattern without almost any difference between both storage positions. Therefore, it can be concluded that the barrel position has not a significant influence on the surface area to volume ratio variation in function of the liquid volume.

Based on the (s/v)_n ratio, it is possible to identify two stages of the barrel during ageing: (I) First half period and (II) Second half period. Since the objective of this work is basically focused on diminishing the volume loss and cask deterioration during ageing, it is highly advisable to keep the barrels in stage (I) thus avoiding as much as possible the stage (II).
Therefore, the optimized criterion for filling volume and re-filling time of wood casks will be restricted to the stage (I) range analysis.

When the hogshead barrel is full (100% filled), the calculated (s/v)₀ ratio was 8.882 m-1 ≈ 90 cm²/L [Table 3] which is consistent with the reported value [11]. However, when the liquid volume in the hogshead barrel decreases (let’s say, due to evaporation losses), the (s/v) ratio diminishes under this initial value (dash line). Based on [Figure 2], when the hogshead barrel is at half capacity (50%), the (s/v)_n ratio is equal to the initial value as the volume and surface area are both proportionally reduced to 50%.

On the other hand, if the volume of liquid decreases below the 50% of the total capacity of the barrel, the (s/v)_n ratio abruptly increases following an exponential trend which (as previously discussed) reach an infinite value when V_n = 0. Since the volume loss during ageing is a direct function of the (s/v)_n ratio, it is expected that below the 50% of the hogshead barrel capacity the evaporation rate will increase also following the same tendency. Therefore, it can be stated that at 50% of capacity, the barrel reaches a critical volume of liquid, a sort of an inflection point. Under that liquid volume, the evaporation losses will be significantly higher also leading to a fast deterioration of the barrel mechanical integrity due to the wood stave’s desiccation process.

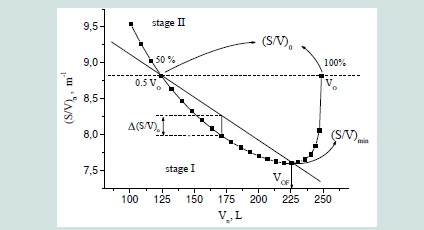
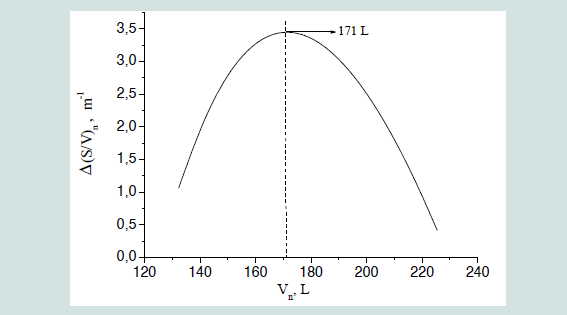
[Figure 3] shows a magnification of [Figure 2] focused on the stage (I) range of the hogshead barrel. The stage (I) comprises also interesting aspects to take into account for the optimization analysis. However, at the beginning, even when the liquid volume decreases just a few liters, the (s/v) value abruptly diminishes to reach a minimum (optimal) value. In the hogshead barrel (250 L), the minimal (s/v)_min value is equal 7.624 m^-1 and this value is reached when the liquid volume in the barrel is V_OF= 225 L (see table 3).

With 10% less of the total barrel capacity, the (s/v)_n ratio decreases approximately 14 %. After this minimal point, the (s/v)_n ratio increases as inverse function of the liquid volume but with a significant less abrupt slope compared with the (s/v)_n ratio change found from 250 to 225L.

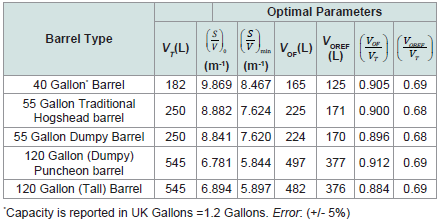
Regarding the impact of the (s/v)_n ratio on the volume loss, at the optimal value of (s/v)_min, the barrel will suffer from minimal volume loss due to diffusional evaporation. Therefore, each barrel has an optimal operational capacity or optimal filling volume (VOF) in which the diffusional evaporation loss finds a minimum. The optimal filling volume was calculated for the different whisky barrels assessed (Table 2) and values are presented in [Table 3].

From this result, a conclusion can be derived: instead of filling it to 100%, it is better to fill the barrel till its optimal volume (V_OF) to be stored in the cellar for spirit ageing in order to reduce the diffusional evaporation losses. This last statement and its demonstration will be discussed later on.

Filling a barrel below its full capacity could seem to be a contradictory idea, because it reduces the space yield efficiency used in the cellar. However, according to the experience of traditional spirit producers, a small air space is empirically left during cask filling in cellars to counteract the pressure changes due to the liquid

expansion and contraction in function of the temperature fluctuation and also potentiate the gas-liquid contact interface for oxidation reactions during maturation which in turn improves the organoleptic attributes of the rum. Nevertheless, apart of the applied empirical approaches which are very specific for each producer, the effect of the barrel filling volume and the re-filling time on the volume loss during spirits maturation has not been clearly elucidated so far and the subject is still under discussion among spirit producers

From Figure 3, it is noticeable that the evaporation loss from V₀ to V_0F occurs in a faster way compared with the liquid volume reduction from V_0F to 0.5 V₀ which is in line with the equilibrium concept.

Additionally, rum producers in Cuba locally report a relative increment of the evaporation loss for short-term (less than 15 months) aged products which it is in line with the (s/v)_n vs V_n pattern observed in [Figure 3].

The barrel will tend to reach the minimum as it is not in the optimal point when it is full. As it will mathematically modelled and discussed later, the evaporation loss rate in the range of V₀ - V_0F (250- 225 L) volume change period is significantly higher than for V_0F to 0.5 V₀ (225-125 L) period. Thus, the analysis has to be conducted to see if it is beneficial to fill the barrel fully since the liquid will be rapidly evaporated and is lost anyway.

Another objective in this work is the optimal refilling time of the barrel during maturation. From Figure 3, it can be deducted that the refilling volume for a barrel is located in the region of V_0F to 0.5 V₀ (225-125 L in the case of the hogshead barrel). The optimal volume for barrel refilling (V_OREF ) can thus be mathematically determined.

Drawing a line between coordinates points [(s/v)_min; v _of] (Figure 3) and calculating the difference at each volume Vn in the barrel between the curve and the line as the optimization function, the inflection point in the curve trajectory indicates the optimal refilling volume which will be observed at the maximal difference Δ (s/v)_max [Figure 4].

In this case, for the traditional hogshead barrel, the optimal refilling volume (V_OREF) was found at V_OREF = 171 L (+/- 8.6 L). This indicates that when the barrel reaches this volume, it is the moment to re-fill it in order to keep the evaporation loss controlled and preserve the barrel’s mechanical integrity.

In Table 3, a summary of the optimal parameters for casks filling and re-filling volume determined for different types of whisky barrels used for rum production are presented. As reported in [19-21], the smaller the barrel size, the higher is the (s/v)₀ value. The shape of the barrel (dumpy or tall) also modifies the (s/v) value. For dumpy shape (more like a square cylinder) the calculated (s/v)₀ value is slightly lower than for the all-shaped designs. Furthermore, the same applies for the (s/v)_min parameter.

An important aspect to notice from [Table 3] is that independently of the found differences between optimal parameters of the barrels (which in turn depends on the relative barrel dimensions) it can be assumed for practical purposes that the minimal value of (s/v)_n ratio for a typical barrel is when the cask is about 90% filled (+/- 5% of error based on the accuracy of the simplified formula to calculate r (Eq.(3) and the optimal volume for re-filling is when the barrel losses are around 30% of its total capacity.When the optimal re-filling volume of a barrel is determined and the evaporation loss percent in the cellar has been established by experimental/empirical studies, the re-filling time can be then defined.

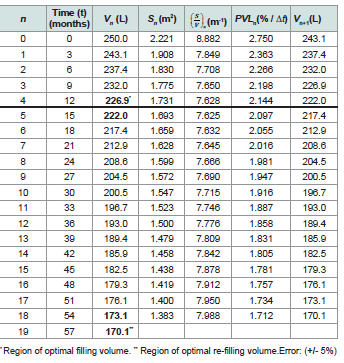
In order to clarify the method, an example of a numerical calculation approach to determine the optimal re-filling time is presented. Calculation results are presented in [Table 4] under the following conditions:

a) Barrel type: (55-Gal Hogshead whisky barrel/ 250 L) b) Product: ‘base rum’ (52-55 % v/v) b) Maximal percent of evaporation loss at full barrel: 11 %/ year (Caribbean region) c) Temporal discrete step for the refilling time calculation: Δt = 3 months (1/4 of year) Similar to the numerical Euler’s method, the first row (n = 0) in Table 4 is completed with the initial values calculated at full barrel conditions V0 = 250 L. The initial partial volume loss PVL_n in 3 months (t = n . Δt) is then: PVL_n =11/4= 2.75 % of the volume loss / 3 months Since the diffusional evaporation is a linear function of the contact surface area [28, 29], the partial volume loss after a Δt of time PVL_n for (n> 0) is calculated by Eq. (16).

to evaporation taking the whole 56 months period as reference can be calculated as

As presented above, a 11% / year of volume loss was considered at full barrel. However, the average value after 56 months was about a 40 % lower. This is in line with internal statistics and empiric criteria of Cuban rum producers about the influence of the ageing time in yearly volume loss percent. Also, the average evaporation rate (ER(t)) in the whole period can be determined as

On the contrary, if the barrel was filled initially to its optimal filling volume of 225 L (corresponding to 13.2 months by interpolation in Table 4), the refilling time is then (56 - 13.2 = 42.8 months) around 3 years and 7 months.

Thus, from the optimal filling volume, the average of percent of total volume loss per year and average evaporation rate in this period can be calculated as

Comparing both full and optimal initial filling volume, in a long-term ageing process the average loss is reduced in around 0.15 L/month-barrel which represents just 0.6% less than the yearly evaporation loss at initial full barrel. In conclusion, for long-term maturation, the effect of the initial barrel filling volume on the evaporation loss reduction is not that significant.

However, as it will be demonstrated in the following calculations, short-term evaporation loss during the spirit ageing process is highly affected by the initial filling volume of the barrel. Firstly, if the initial period from full barrel to reach the optimal filling volume of 225 L is analyzed, it is possible to find significant differences. As previously mentioned, by interpolation, the time to reach the 225 L from hogshead full barrel is 13.2 months and the averaged percent of volume loss per year and evaporation rate in this ageing period are respectively

In this first period of approximately one year, the average percent of volume loss per year and the evaporation rate are about 35 % higher compared with the whole period of 56 months, thus this is consistent with local reports of Cuban rum producers. The results confirm the influence of the first ageing period on the increment of the total volume loss in cellars. At this point, making an analysis for the short-term ageing process to compare the volume loss reduction if the barrel is filled at optimal volume against the full barrel filling.

Let’s consider a 12 months aged product (n = 4), if the barrel was initially full, the average volume loss and evaporation rate in this period can be calculated as

In a short ageing period, by initially filling the barrel at optimal volume, the percent of evaporation loss can be reduced approximately 87% compared with the percent of volume loss at full barrel filling in the same ageing period (12 months in this case). That represents a saved volume of around 5.2 L/year-barrel (hogshead barrel). Thus for 100 barrels in the cellar, 520 L of product can be saved from evaporation per year. The same calculation method can be conducted for other barrels types and cellar specific conditions. Beyond the theoretical results, the proposed method needs to be adapted for practical purposes and then efficiently applied in different scenarios of spirit industry according to the specific features of each producer such as cellar environmental conditions, ageing technology, cask management strategy among others. Indeed, other math models can be explored and compared with found results in order to increase the calculation accuracy for different types of barrels.

The (s/v)_n ratio of a barrel during ageing constantly changes in function of the volume of liquid and therefore the ageing time. This parameter will range from a constant value (barrel completely filled), which certainly depends on the cask size, to a final value that will tend to infinity when the volume of the liquid contained in the barrel approaches to zero.

Found results demonstrated that for traditional barrels within a capacity range of 182-545 L: 1) the (s/v)_min ratio is practically independent of the barrel storage position (horizontal or vertical). 2) the (s/v)_min ratio and therefore its minimal diffusional evaporation loss is established when the barrel is around 90% of its total capacity during short-term (less than 15 months) maturation process. 3) instead of filling the barrel to 100%, it is better to fill the barrel till its optimal volume (V_OF) to be stored in the cellar for spirit ageing in order to reduce the diffusional evaporation losses. 4) in order to avoid cask deterioration during long-term spirit maturation, the barrels have to be re-filled when the liquid volume reaches 70% of the total barrel capacity. 5) for long-term (more than 3 years) ageing process, the initial filling volume of the barrel does not have a significant influence on the average evaporation loss reduction. 6) in a short ageing period, by initially filling the barrel at optimal volume, the percent of evaporation loss can be reduced approximately 87% compared with the percent of volume loss at full barrel filling in the same ageing period. The presented study might be useful not only for rum producers but for other specialists and researchers in the production of aged spirits. The proposed method needs to be adapted for practical purposes and then efficiently applied in different scenarios of spirit industry according to the specific features of each producer such as cellar environmental conditions, ageing technology, cask management strategy among others.

N. del Toro del Toro and H. Crespo Sariol: conceptualisation, formal analysis, writing - original draft, validation; N. del Toro del Toro and J. AyánRial:investigation, methodology, visualisation; H. Crespo Sariol, J. Yperman, D. Vandamme: project administration, resources, supervisionJ. Yperman, D. Vandamme, R. Carleer and H. Crespo Sariol: analysed the calculation methods and math models, writing - review and editing.

The authors would like to thanks the VLIR-UOS project between Belgium and Cuba for providing funding and granting the support of the current and future studies.
Conflicts of Interest: The authors declare no conflict of interest.
Compliance with ethical standards: The authors declare that the submitted work is original and is not published elsewhere in any form or language, following the rules of good scientific practice and maintaining the integrity of the research and its presentation.